Simulation Techniques: Acoustical Engineering via Various Expansion Techniques

In previous articles, I have demonstrated how analytical approaches can be superior to numerical ones, when it comes to calculation speed, gathering insights into the physics, and how they can be combined with numerical simulations to get the best of both worlds. Sometimes the result is directly an analytical expression in which you enter some parameters for the geometry and medium and the output is, for example, a sound pressure. Other times a model is made by a manual mapping of certain continuous parts in a physical model to a reduced order lumped model with a finite number of masses, springs, and resistance that captures the physical behavior of the full system to some degree.
 
This requires some insight into the physics of the systems, and experience with building such lumped models in general. In this article we will look at such “macromodelling” from a different perspective than this traditional lumped modelling. The models found here directly follow from the mathematical description of the physical problem, and as some mathematical approaches lend themselves well to a circuit implementation, the mapping from physical system to model is done entirely in the realm of mathematics.

Taylor Series Expansion
A Taylor series is probably one of the most well-known approaches to simplifying an engineering problem. Here, you approximate some function f as a function of x with a general infinite series as:
  Each prime represents a differentiation, and here the special case of finding the derivatives for the function at x=0 is chosen, in which case the series is denoted a Maclaurin series. This is chosen since when a dynamical system is considered, there is often an interest in finding the system behavior at low frequencies, with x proportional to the frequency.

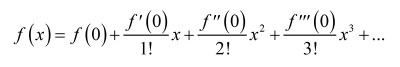
A case of interest in microacoustics is a tube of equilateral triangular cross-section for which the low-frequency behavior described via a rather involved expression for the series impedance [1] can be approximated with just two components via a Taylor series truncated to a low order with a cross-sectional area S and a short length l with additional variables not important for the discussion at hand as:
 
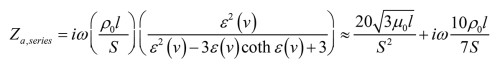
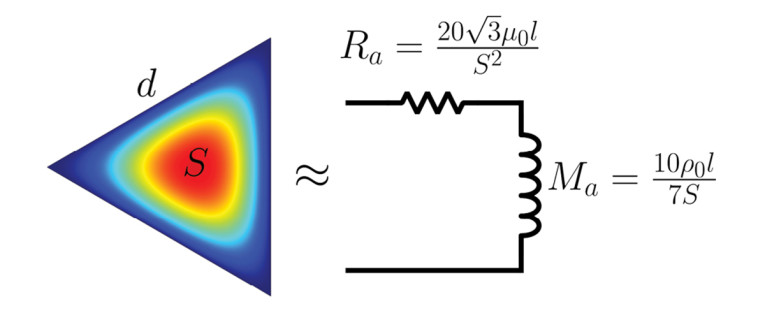
This result is essentially a resistance due to viscosity and an acoustic mass, as illustrated in Figure 1, such that at low frequencies this complex impedance can be approximated by positive and constant valued components, although this is not always the case. The so-called boundary layer in which the main microacoustics effects take place is seen to fill out most of the cross-section at the assumed low frequency, whereas for higher frequencies this boundary layer thickness decreases.
  The cross-section shown in Figure 1 is of particular interest to me as I was the one that found these component values for the series and shunt immittances [2]. While these approximations only hold for low frequencies, it will be shown in a later section how I have now found complete circuits for not only this cross-section, but also for the prototypical “slit” or “layer” geometry.

Asymptotic Expansion for Large Arguments
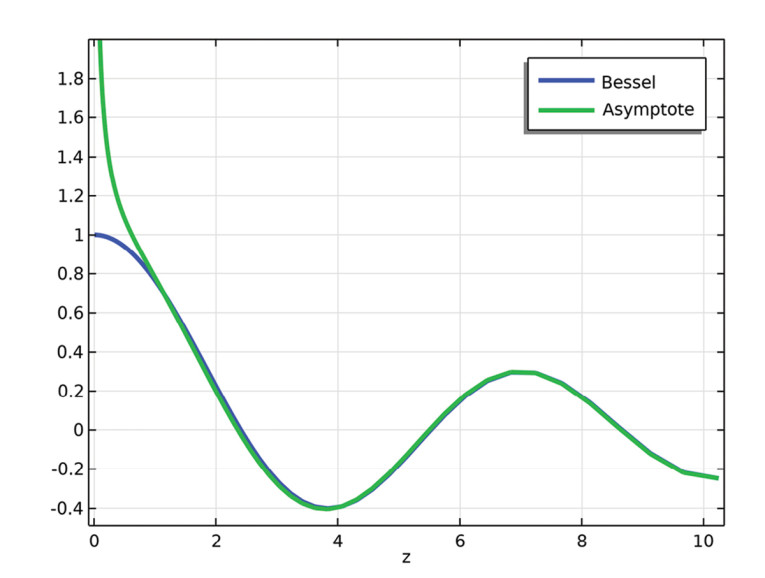
While the Taylor series often is used for getting insight at low frequencies, it can also be informative to know the general behavior of a response toward higher frequencies, which is sometimes termed asymptotic expansion, with our specific interest being the behavior toward infinity. As an example, we can look at the Bessel function of first kind and zeroth order below, where an approximation is given as [3]:
  The exact Bessel function is compared to this approximation in Figure 2 for a real argument with z representing here the frequency. If an asymptotic expansion can be found, it will typically be simpler than the exact expression and so may be more easily interpreted and/or modelled in subsequent setups. However, as asymptotic behavior toward high frequencies is potentially frequency-dependent beyond what can be modelled with standard components, it may not be readily implemented in electrical circuit simulation software.

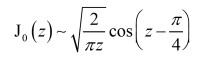
With the described approximations limited to either low or high frequencies, there will be an intermediate frequency range often of importance, where these models will not accurately capture the physical behavior. The models are, however, often (mis)used outside their range of validity in engineering, either because their limitations are not realized, or because an inaccurate model is better than no model. In the following sections, we will look at more elaborate lumped models that can capture the physical behavior across wider frequency ranges.
 
Padé Approximant Expansion
The so-called Padé Approximants can be a better choice than the Taylor series expansion, especially when there is obvious zero and pole behavior in the exact expression. An example can be shown for the equilateral triangular cross-section again, where a Padé Approximant of order [2,1] can approximate the series impedance for a short tube with length of l, area S, and side length d as:
 
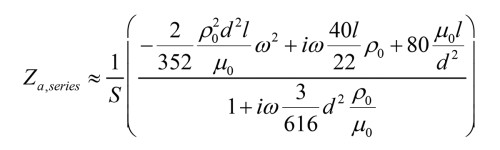
This will better approximate the exact expression than the Taylor series expansion as seen in Figure 3 for the normalized real part of the series impedance. A network can be synthesized from here as shown in Figure 4 that perfectly fits the Padé Approximant expression, where in general the Padé approach will lead to so-called Foster networks [4].
 
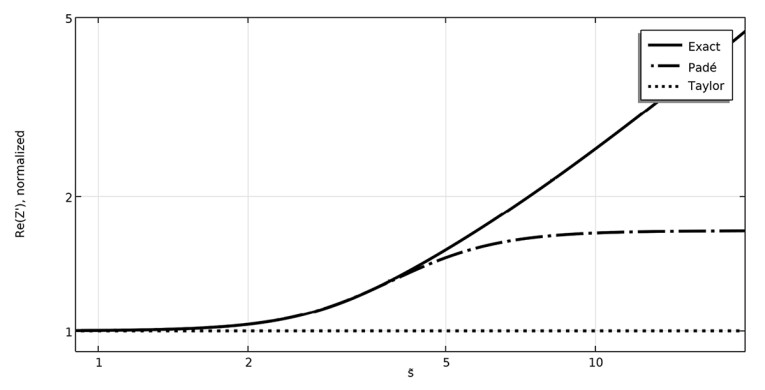
The network presented in Figure 4 is from an upcoming paper for the Journal of Acoustical Society of America (JASA), where the Padé Approximant approach is used for finding series and shunt immittances for this triangular cross-section, the circular cross-section, and the slit/layer. However, such circuits are naturally truncated based on the initial choice of Padé orders, and if a better approximation is sought using a higher order, a new circuit must be synthesized, and all component values must be fitted to this new circuit. It turns out that for the three cross-sections in question, a more elegant solution exists that makes it trivial to expand the resulting circuits to any order.
 
Continued Fraction Expansion
Continued Fractions represent a systematic and canonical way of representing numbers or functions. This is probably best shown via an example. Imagine that you are working on an electrical circuit where a resistor must be 1.39Ω. This is not a standard value in the E-series for resistors, so you cannot just pick it from the drawer. You might get close, but not with an exact match from a single resistor. Now, imagine that you are further constrained in that you only have access to 1.2Ω resistors, although as many as you want. Can you construct a resistor network that will realize exactly the desired resistance from combining the available resistors? I don’t think the answer is trivial, but in fact, you can. When writing the resistance as a continued fraction in terms of 1.2Ω resistors, an exact match of value can be found as:
  The red numbers hint to the network implementation as it is shown in Figure 5. It takes 16 resistors to reach, but the nominal value is exactly the desired 1.39Ω.
  Note that there is nothing special about 1.39 other than that it is rational number, and neither is the resistor value of 1.2 specially chosen. A rational number like the desired nominal value whose decimal expansion either terminates or repeats with a finite sequence (such as 2/3=0.666…) can always be constructed via such a finite continued fraction and a finite circuit to boot. An irrational number would correspond to an infinite continued fraction, but with proper truncation, any desired precision can be obtained in such cases. So, should you need a resistance of π, there is a way to approximate it with a continued fraction-based network. You of course must consider the cost of this amount of resistors, alongside a sensitivity analysis for a given tolerance on the components, but if a particular nominal value is needed, there is a way to get there, and you will have a reference for when you potentially go with a simpler circuit later in the development process.

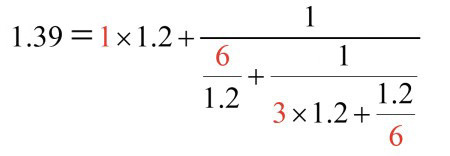
The continued fraction approach really shines when it represents a function instead of simply a number. In engineering, the relevant functions are typically complex with complex arguments. Some functions lend themselves well to a continued fraction approach, such as the hyperbolic tangent, which can be written as:
 
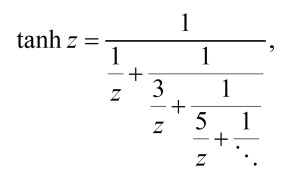
This can be utilized in microacoustics where such hyperbolic functions may appear in the general series and shunt immittances for the acoustic field in narrow slits and tubes with viscous and thermal losses included. Consequently, infinite networks can be established to represent the series impedance and shunt admittance. The resulting networks are of the so-called Cauer type [4] with alternating series and shunt components. Adding extra branches does not require recalculating previous components in this canonical form, which is a major advantage compared to alternative techniques. More components are needed if the highest frequency of interest increases, and more sections of this network are needed if the tube is longer, but while convergence might be slow, any desired accuracy can be achieved in a simple algorithmic approach.

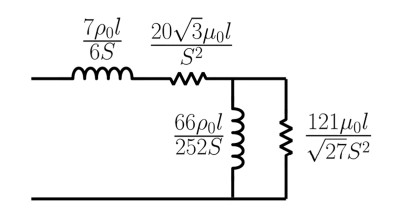
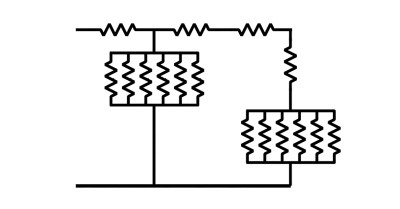
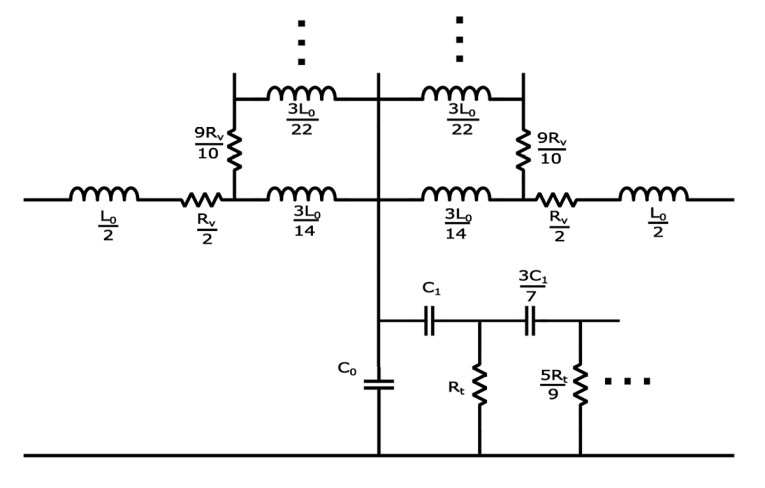
I recently developed these immittance circuits for the rectangular slit and for tubes with equilateral triangular cross-sections, and this research was recently presented in JASA [5]. The general circuit for a short tube length with equilateral triangular cross-section is shown in Figure 6, where both series and shunt impedances are included, and a similar circuit was found for the slit structure. These circuits can be expanded to infinity, and thus an accurate model can be had to any desired frequency. This work can be seen as a conclusion of decades of research into lumped representations of the thermoviscous effects in tubes and slits, but the continued fraction expansion approach can also be utilized in other scenarios where similar skin-effects are present. An example of this is the electromagnetic behavior in a loudspeaker, and this will be investigated now, although with an alternative expansion technique.
 
Partial Fraction Fitting Expansion
If you know some transfer function in analytical form, you have several avenues to explore it as shown in previous sections. But what if the transfer function cannot be known analytically, for example if it is a measured or simulated response with numerical values only? Partial Fraction Fitting to the rescue! This function was implemented in COMSOL Multiphysics last year, and it can analyze complex input data and output fitted partial fractions that approximate the input to essentially any desired degree. The general mathematical setup consists of an asymptotic part Y∞ alongside real and complex conjugate poles, ξ’s and ζ’s, respectively, with their respective residues R and Q as:
 
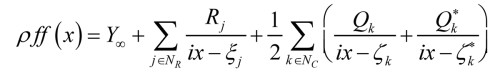
Here, x is the standard frequency as opposed to the angular frequency often used when dealing with impedances and transfer functions. The equation is one of several alternative forms in which a rational function can be written, and this partial fraction form is for example very convenient for conversion into time-domain responses, with more details in recent blog post of mine [6]. The approach for utilizing a partial fraction could be utilized for the microacoustics cases, and I plan on doing that in a third JASA paper, but here I will instead illustrate the method for a loudspeaker example from the COMSOL Application Library [7], investigating a lumped circuit representing the blocked electrical impedance of the loudspeaker magnet system shown in Figure 7.
 
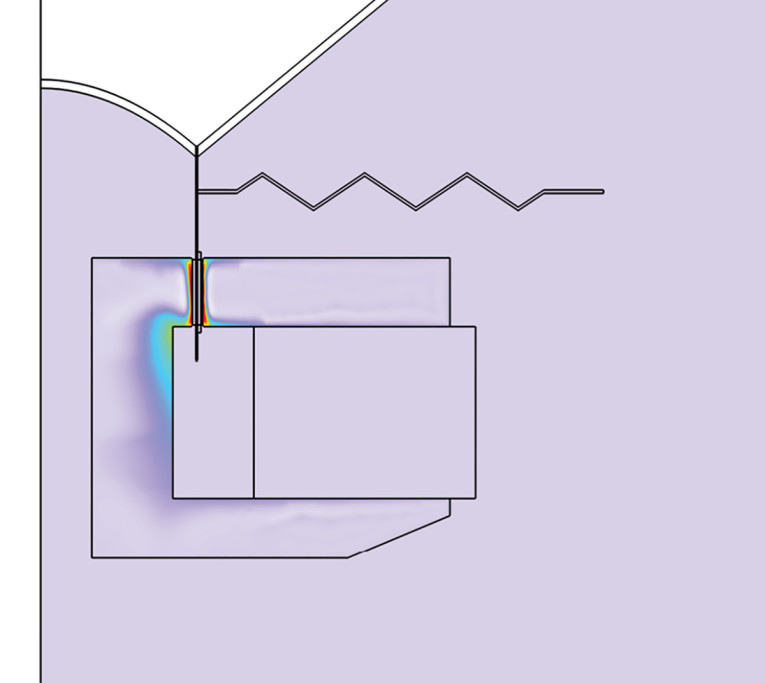
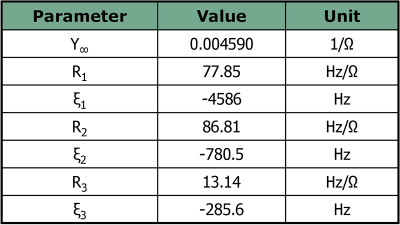
A frequency sweep is performed for this finite element method (FEM) setup and the complex blocked impedance is calculated over a frequency range chosen such that it captures the overall characteristics of the magnet system. The complex impedance values are put into a table and run through the partial fraction fitting routine to a chosen order and the resulting values are shown in Table 1, where three real poles have been found alongside an asymptotic value. It should be mentioned that the analysis was carried out for the admittance instead of the impedance due to the so-called “properness” of such immittances with more details in my blog post mentioned earlier.
 
The resulting partial fractions for the blocked admittance Y to some order decided under the fitting settings can then be written in their summed form as:
 

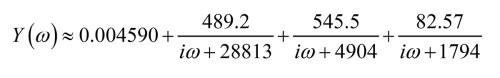
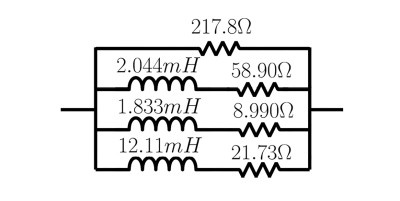
This can be exactly synthesized in a Foster-like circuit form [4] shown in Figure 8 with four resistances and three inductances.
 
The circuit will have an excellent match with the electrical impedance magnitude and phase across the relevant frequency range found via the simulated setup, although this is not immediately obvious when plotting the frequency dependent component values in Figure 9. At low frequencies, the resistances will dominate the overall impedance, and so the deviation in accuracy for the imaginary part of the impedance will be of little importance, which the partial fraction fitting scheme correctly “identifies.”
 
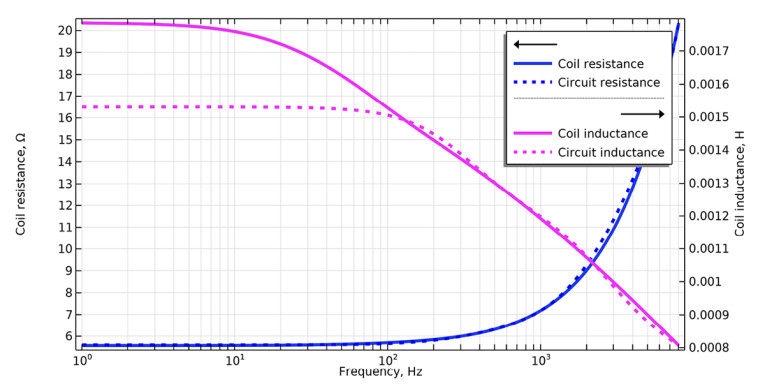
Starting with a numerical solution, we essentially achieve an approximate numerical transfer function and subsequently synthesize a network with positive and frequency independent component values. If instead of having a numerical setup an analytical expression was known for the impedance, one could take, for example, a continued fractions route, but for many complex simulation cases, a numerical output is the only available information. The partial fraction fitting approach can also be applied to the analytical microacoustics solutions, and the network found will be different from both the Continued Fraction network and the Padé ditto. Network synthesis is not unique, and it is very interesting to work with these different methods for some common cases that can be solved with several approaches and explore the strengths and weaknesses of each approach.

Closing Comments
It can be extremely valuable to have some classical mathematics and/or physics knowledge when solving engineering problems, instead of just trying to solve them via a trial-and-error approach or jumping directly to simulation software. If you somehow know that a particular problem must have an analytical solution, you are in a great position to solve the problem, even if it may be very difficult, compared to not knowing whether it is solvable or not.

The example with the resistors combining into a particular nominal value is meant to illustrate this. If it is imperative that you solve this seemingly simple problem, it could be an overwhelming task if you start experimenting with combining resistors and not getting quite the correct value due to the combinatorics involved. If instead you have the knowledge that this fundamentally must have a finite network associated with it, you are in a completely different situation where a solution can be found in a few minutes. Now, scale this up to a more pressing and complex problem, and you can hopefully see how brute force can only take you so far.

Conversely, knowing in advance that a particular approach is not feasible is also very valuable. I have worked with clients that had spent months taking a trial-and-error approach to solve a problem, where I could show with a combinatorics analysis that it would take literally millions of years to solve in this manner due to the number of variables involved and their interdependencies. So, while analytical methods may seem archaic to some and a numerical route is often taken instead, there can be time and money to be saved by being well-versed in various analytical methods. aX

References
[1] M. R. Stinson and Y. Champoux, “Propagation of sound and the assignment of shape factors in model porous materials having simple pore geometries,” Journal of the Acoustical Society of America, Volume 92, No. 2, pp. 685-695, 1992.
[2] R. Christensen, “Lumped Parameter Description of Thermoviscous Acoustics in Tubes with Equilateral Triangular Cross-Sections,” Acta Acoustica United With Acoustica, Volume 105, No. 6, pp. 1283-1285, 2019.
[3] M. Abramovich and I. A. Stegun, Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, New York: Dover, 1972.
[4] E. A. Guillemin, Synthesis of Passive Networks, John Wiley and Sons, 1977.
[5] R. Christensen, “Circuit models for thermoviscous acoustics in waveguides of various cross-sections via continued fractions,” Journal of the Acoustical Society of America, Volume 156, No. 6, p. 3930–3942, 2024.
[6] R. Christensen, “Exploring the Partial Fraction Fit Functionality in COMSOL Multiphysics,” August 15, 2024, www.comsol.com/blogs/exploring-the-partial-fraction-fit-functionality-in-comsol-multiphysics
[7] COMSOL, “Loudspeaker Driver — Frequency-Domain Analysis,” www.comsol.com/model/loudspeaker-driver-8212-frequency-domain-analysis-1369

This article was originally published in audioXpress, April 2025